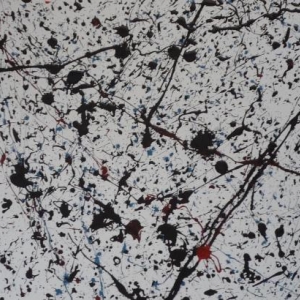
SPA La technique du dripping

Dans le cadre des journées des Musées, l’établissement de la Ville d’eaux avait organisé une animation tentant d’expliquer la technique du dripping ("goutte à goutte") et de proposer aux visiteurs de s’y exercer. Nombreux, jeunes et moins jeunes, se sont attachés à réaliser une « œuvre » selon les principes définis par celle-ci.et ce, avec plus ou moins de bonheur. Quels sont-ils ? En 1947, Jackson Pollock abandonne l'utilisation classique du pinceau pour d'autres techniques le dripping (goutte à goutte) et le pouring (coulée). De sorte que le peintre n’entre plus en contact direct avec la toile, posée au sol, qu’il peint dans le plan horizontal et non plus sur une surface verticale, qu’il laisse couler la matière picturale (qu'il liquéfie au maximum) directement du pot ou la projette sur la toile à l'aide d'un bâton, d'un pinceau ou d'autres outils, et qu’aucune partie de la toile n'est privilégiée. A la fin des années 90, Richard Taylor, un physicien américain (Université d'Oregon) passionné d'art a analysé 5 œuvres de Pollock et il y a décelé une structure géométrique de type fractal. Très complexe à comprendre, cette notion est étroitement liée à la théorie du chaos. Ainsi, lorsqu’on quadrille une toile de Pollock et qu'on analyse chaque partie de cette toile, on constate que les différentes couleurs sont présentes dans des proportions similaires pour chacune des parties (36 % pour le noir, 12 % pour les autres couleurs) et donc pour la toile toute entière. Cette autosimilarité est propre à Pollock car il ne calculait rien à l'avance mais il maîtrisait la coulée de peinture : Cette particularité permet d'ailleurs de déceler les faux-Pollock ! C'est probablement cet équilibre imperceptible qui flatte l'œil et contente notre cerveau lorsque l'on observe une œuvre de Jackson Pollock (1912-1956). Qu’est la fractale ? C’est une forme géométrique infiniment fragmentée qui a pour caractéristique que chaque partie d'un ensemble possède, à n'importe quelle échelle, une apparence semblable à l'ensemble. Chaque forme fractale possède donc une superficie définie mais un périmètre infini. Ainsi, le chou-fleur est l'un des nombreux éléments naturels (végétaux ou minéraux) qui illustre le mieux le principe des fractales et la notion d'autosimilarité : un certain nombre de parties sont similaires au tout mais dans des proportions différentes : le chou-fleur est composé d'une série de fleurs, elles-mêmes composées de plus petites fleurs, semblables au chou-fleur entier. Cette notion se retrouve aussi dans "La vache qui rit" où cette idée de " parties semblables au tout " peut être comprise de manière très basique par cette publicité. On y voit une vache portant une boucle d'oreille. Cette dernière présente la même image : une vache portant une boucle d'oreille et ainsi de suite… jusqu'à l'infini ? C'est probablement cette notion d'infini qui fascine les créateurs d'images fractales réalisées avec l'aide de puissants logiciels mathématiques
Le Musée de la Ville d'eaux possède quelques toiles abstraites dont une œuvre de David DEHAM (Tournai, 1967) huile sur papier collé sur unalit ( don de l'artiste en 1998 ).
( Photos sur www.ardenneweb.eu )
François DETRY